terça-feira, 15 de dezembro de 2015
quarta-feira, 28 de outubro de 2015
sábado, 10 de outubro de 2015
sexta-feira, 9 de outubro de 2015
sábado, 26 de setembro de 2015
quarta-feira, 16 de setembro de 2015
quarta-feira, 2 de setembro de 2015
domingo, 30 de agosto de 2015
sábado, 15 de agosto de 2015
terça-feira, 11 de agosto de 2015
sexta-feira, 29 de maio de 2015
quinta-feira, 28 de maio de 2015
quarta-feira, 27 de maio de 2015
sexta-feira, 6 de março de 2015
DIFERENÇA ENTRE GEODÉSIA E TOPOGRAFIA:
DIFERENÇA ENTRE GEODÉSIA E TOPOGRAFIA:A Topografia está inserida na Geodésia, utilizam métodos e instrumentos semelhantes, porém, a Geodésia se preocupa com a forma e dimensões da Terra, enquanto a Topografia se limita a descrição de área restritas da superfície terrestre.
A GEODÉSIA (do grego daiein , dividir) é uma ciência que tem por finalidade a determinação da forma da terra e o levantamento de glebas tão grandes que não permitem o desprezo da curvatura da Terra. A aplicação da Geodésia nos levantamento topográficos é justificada quando da necessidade de controle sobre a locação de pontos básicos no terreno, de modo a evitar o acúmulo deerros na operação do levantamento.
É a parte da MENSURAÇÃO que tem por objetivo e estudo da forma e dimensão da terra. Levando em consideração a forma da Terra, a Geodésia desenvolve as soluções para transformar a superfície do elipsóide em uma superfície plana como a das cartas.
Apesar da superfície terrestre ser bastante irregular, formada de depressões e elevações, é possível considerá-la regular em face da reduzida dimensão destes acidentes em relação ao raio da Terra, uma vez que a máxima depressão ou elevação é inferior a 10 km, desprezível ante a extensão do raio médio da Terra, aproximadamente igual a 6.371 km. Nestas condições, em primeira aproximação, a superfície terrestre pode ser considerada como a superfície de nível médio dos mares, supostamente prolongada por sob os continentes e normal em todos os seus pontos à direção da gravidade, superfície esta denominada de GEÓIDE.
Tendo em vista a impossibilidade de ser determinada a equação analítica representativa desta superfície, adotou-se como forma da Terra a de um elipsóide de revolução girando em torno do seu eixo menor, dito ELIPSÓIDE TERRESTRE (figura), que é definido por:
SEMI-EIXO MAIOR = a
ACHATAMENTO: A = (a – b) / a
Elipsóide internacional de referência:
a = 6.378.388 m
b = 6.356.912 m
A = 1/297
R = (2a + b)/3 = 6.371.220 m
Assim sendo, a GEODÉSIA1 e a TOPOGRAFIA têm os mesmos objetivos,
diferindo nos fundamentos matemáticos em que se baseiam, a geodésia apoiada na trigonometria esférica e a topografia, na trigonometria plana.A TOPOGRAFIA por sua vez, que considera trechos de dimensões limitadas,
admite a superfície terrestre como plana, o que corresponde a desprezar a curvatura da Terra.
No nosso curso nos aprofundaremos no estudo da GEODÉSIA.
É sob este conceito de forma da Terra que a GEODÉSIA trabalha nos estudos que exigem maior rigor matemático.
DEFINIÇÃO DE RUMO, AZIMUTE
DEFINIÇÃO DE RUMO, AZIMUTE, DEFLEXÃO, ÂNGULO HORÁRIO
e ANTI-HORÁRIO, INTERNOS e EXTERNOS:
– RUMO:
Rumo de uma linha é o menor ângulo horizontal, formado entre a direção NORTE/SUL e a linha, medindo a partir do NORTE ou do SUL9, no sentido horário (à direita) ou sentido anti-horário (à esquerda) e variando de 0o a 90º ou 0g a 100g.
Se tomarmos para exemplo da figura 3.1, e se dissermos simplesmente que seu rumo é 45o00’ (menor ângulo horizontal formado pela linha A-B e a direção N/S). Portanto, não teremos bem caracterizada a posição relativa da linha, pois esta poderá ser entendida como sendo NE, NW, SE ou SW.
Uma vez que esta poderá ser localizada de quatro maneiras diferentes em relação a direção NORTE/SUL, será necessário indicar qual o quadrante. Para o exemplo da figura 3.1 será:
Sentido: de A para B, portanto o menor ângulo, que representa o rumo da linha AB será medido a partir do Norte (N) no sentido horário, para o Leste (E).
Orientação: 45°. Podemos dizer que o RAB = 45º NE. Extensão: 20,00 metros.
Observando a figura 3.2, concluiremos que:
● A-1 = 36o NE
● A-2 = 46o SE
● A-3 = 28o SW
● A-4 = 62o NW, são rumos vantes.
Já os rumos das linhas:
● 1-A = 36o SW
● 2-A = 46o NW
● 3-A = 28o NE
● 4-A = 62o SE, são rumos à ré.
Observamos que o RUMO RÉ de uma linha é igual ao valor numérico do RUMO VANTE, situado em quadrante oposto.AZIMUTE:
Azimute10 é o ângulo horizontal formado entre a direção Norte/Sul e o alinhamento em
questão. É medido a partir do Norte, no sentido horário (à direita), podendo variar de 0º
a 360º ou 400 g.
Usualmente, quando não for expressamente afirmado o contrário, o AZIMUTE será sempre à direita (sentido horário) do NORTE. Numa definição mais ampla, o azimute pode ser medido do NORTE ou do SUL no sentido horário (à direita) ou no sentido anti-horário (à esquerda)..
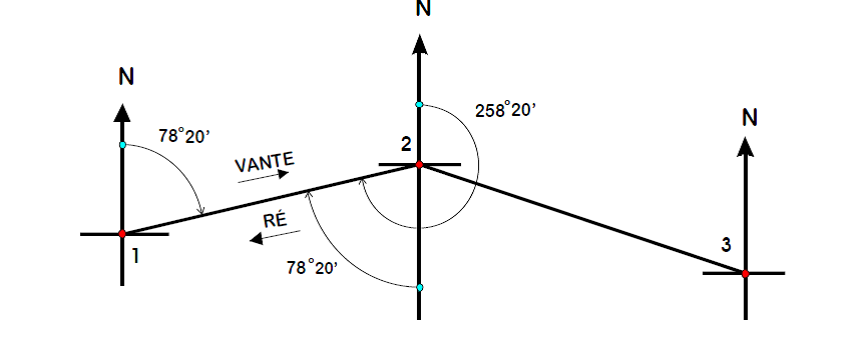
Na figura 3.3, estaremos relacionando os rumos da figura 3.2 com os
AZIMUTES.
Portanto os AZIMUTES VANTES das linhas:
● = A−1 Az 36º00´
● = A−2 Az 180º00´– 46º00´ = 134o00´
● = A−3 Az 180º00´+28º00´ = 203o 00´
● = A−4 Az 360º00´-62º00´ = 298o00´
RÉ, é dado pela expressão
AZIMUTE À RÉ (1-2) = AZIMUTE À VANTE (1-2) ± 180o
Conversão entre RUMOS e AZIMUTE:
QUADRANTE FÓRMULA
NE → RUMO = AZIMUTE(*)
SE → RUMO = 180o – AZIMUTE
SW → RUMO = AZIMUTE – 180o
NW → RUMO = 360o – AZIMUTE
(*) NOTA: Valor numérico do Rumo será igual ao valor numérico do Azimute.
Quando transformamos de Azimute para Rumo não podemos esquecer de indicar o quadrante.
DEFLEXÕES:
Deflexão é o ângulo formado entre o prolongamento do alinhamento anterior e o alinhamento que segue. Varia de 0° a 180° e necessita da indicação da direita (sentido horário) ou da esquerda (sentido anti-horário) (figura).
CÁLCULO DOS AZIMUTES SENDO DADOS AS DEFLEXÕES:
Observando a figura 3.6, pode-se afirmar:
Az2-3 = Az1-2 + Dd2-3 (3.2)
Az3-4 = Az2-3 - De3-4
Onde: Az = azimute das linhas;
Dd e De = Deflexões à direita e à esquerda
Exemplo:
Dados: Az1-2 = 59º20’20”
Dd = 55º30’25”
De = 89º35’40”
Calcular Az2-3 = ?
Az3-4 = ?
Utilizando as equações (3.2) e (3.3) determina-se:
Az2-3 = 59º20’20” + 55º30’25” = 114º50’45”
Az3-4 = 114º50’45” – 89º35’40” = 25º15’05”
CONDIÇÕES DAS CURVAS DE NÍVEL
CONDIÇÕES QUE AS CURVAS DE NÍVEL DEVEM REUNIR:
Para completar o tema, temos de dizer que as curvas de nível podem adotar as mais diversas formas, consoante a configuração do terreno, mas todas elas têm de ter determinadas condições, que, a seguir, vamos enumerar e que temos de ter em conta quando vamos desenhar o plano:
• Toda curva de nível devem ser cheias (linha contínua) e ser fechada (figura
Duas curvas de nível de cotas diferentes não podem cortar-se, porque disto resultaria um único ponto com duas cotas diferentes, o que é um absurdo. (figura).
cota 500 e 600 para um mesmo ponto.
Duas curvas de nível não podem se encontrar e continuarem numa só, porque teríamos duas curvas de nível superposta e para isto acontecer deveríamos ter um plano vertical. Vemo-nos então perante uma escarpa.
Quando o terreno é de rocha viva, chama-se escarpado. Neste caso as várias curvas podem chegar a ser tangentes (figura).
Representar as curvas múltipla de 5 ou de 10 metros com traços mais fortes, assinalando o valor das cotas somente nestas curvas (somente curvas de cotas inteiras). (figuras a esquerda e figura a direita )
Quando não é possível fechar-se o desenho de certa curva de nível dentro da planta por causa das dimensões do papel, deve-se anotar o valor de sua cota em ambas as extremidades da curva. Caso ela se feche dentro dos limites do papel (margem), então anota-se o valor de sua cota sobre a própria linha (figura).
Quando uma curva de nível atravessa uma região do levantamento em que não pode ser determinada (leito do rio, edificações, etc.), pode nessa travessia, deixar de ser traçada ou ser figurada por linha interrompida.
• Pela figura vemos que trata-se de um vale. O que é impossível é fundo do vale coincidir com a cota 37 em toda sua extensão, ou seja, tratar-se de um vale cujo fundo ("talveg") é horizontal para esquerda e para a direita.
Não existe terreno com esta forma, mesmo porque, se fosse o caso, as águas da chuva ficariam retidas e formaria um lago no local.
Uma curva de nível não pode bifurcar-se.
• Se por um ponto da curva de nível traçarmos uma perpendicular à tangente a esse ponto, essa perpendicular representará até chegar a outra curva de nível a linha de maior inclinação do terreno (figura )
As curvas de nível nunca se interrompem bruscamente (figura) Nenhuma curva de nível pode desaparecer ou aparecer repentinamente. Na figura, o terreno na secção AB terá que passar da cota 33 para a 35 sem passar pela cota 34
interrupcao busca
Para completar o tema, temos de dizer que as curvas de nível podem adotar as mais diversas formas, consoante a configuração do terreno, mas todas elas têm de ter determinadas condições, que, a seguir, vamos enumerar e que temos de ter em conta quando vamos desenhar o plano:
• Toda curva de nível devem ser cheias (linha contínua) e ser fechada (figura
cota 500 e 600 para um mesmo ponto.
Duas curvas de nível não podem se encontrar e continuarem numa só, porque teríamos duas curvas de nível superposta e para isto acontecer deveríamos ter um plano vertical. Vemo-nos então perante uma escarpa.
Quando o terreno é de rocha viva, chama-se escarpado. Neste caso as várias curvas podem chegar a ser tangentes (figura).
Representar as curvas múltipla de 5 ou de 10 metros com traços mais fortes, assinalando o valor das cotas somente nestas curvas (somente curvas de cotas inteiras). (figuras a esquerda e figura a direita )
A figura mais a esquerda representa um terreno em curva, porem com inclinacao uniforme e intervalo = 1 metro a figura mais a direita representa um terreno em plano uniformemente inclinado
Quando uma curva de nível atravessa uma região do levantamento em que não pode ser determinada (leito do rio, edificações, etc.), pode nessa travessia, deixar de ser traçada ou ser figurada por linha interrompida.
• Pela figura vemos que trata-se de um vale. O que é impossível é fundo do vale coincidir com a cota 37 em toda sua extensão, ou seja, tratar-se de um vale cujo fundo ("talveg") é horizontal para esquerda e para a direita.
Não existe terreno com esta forma, mesmo porque, se fosse o caso, as águas da chuva ficariam retidas e formaria um lago no local.
Uma curva de nível não pode bifurcar-se.
• Se por um ponto da curva de nível traçarmos uma perpendicular à tangente a esse ponto, essa perpendicular representará até chegar a outra curva de nível a linha de maior inclinação do terreno (figura )
linha de maior inclinacao
As curvas de nível nunca se interrompem bruscamente (figura) Nenhuma curva de nível pode desaparecer ou aparecer repentinamente. Na figura, o terreno na secção AB terá que passar da cota 33 para a 35 sem passar pela cota 34
CURVAS DE NÍVEL
– GENERALIDADES
Curva de nível é uma linha que liga pontos na superfície do terreno de mesma cota (altitude). Esta linha é dada pela intersecção de planos horizontais com a superfície do terreno, sendo uma forma de representação gráfica de extrema importância.
Portanto, as curvas de nível, no sistema que estamos estudando, são dadas pela projeção sobre um plano de referência adotado (para cotas) ou plano Datum (para altitudes) das interseções de superfície física considerada, com planos horizontais eqüidistantes entre si.
Enquanto a planimetria possui uma forma de representação gráfica perfeita, que é a planta (projetada num plano horizontal de referência), onde os ângulos, aparecem com sua verdadeira abertura e as distância exatas, naturalmente reduzidas pela escala do desenho, na altimetria só conta com a representação gráfica em perfil. Mas o perfil só representa a altimetria de uma linha (seja reta,
curva ou quebrada) e não de uma área. Então, a visão geral fica altamente prejudicada, pois precisaríamos de um número imenso de perfis do mesmo terreno em posições e direções diferentes, para termos uma visão panorâmica e nunca poderíamos visualizá-los todos ao mesmo tempo.
A projeção das várias interseções sobre o plano horizontal de referência (plano topográfico), vão nos dar aproximadamente a forma do relevo na árealevantada. A esta plano topográfico com estas curvas desenhadas em escala reduzida é que damos o nome de planta topográfica planialtimétrica.
A interpretação do terreno, representado por curvas de nível na planta, é feita pelas distâncias horizontais que separam as curvas de nível. Curvas de nível muito afastadas umas das outras indicam que a topografia do terreno é suave; se estiverem muito próximas, trata-se de topografia acidentada e, portanto, de terreno fortemente inclinado. Sendo assim, o maior declive de um terreno ocorre no local em que aparece a menor distância horizontal entre duas curvas de nível.
teledetencao
NOÇÕES DE
SENSORIAMENTO REMOTO OU TELEDETENCAO
Entende-se
por Sensoriamento Remoto ou teledetencao a utilização conjunta de modernos sensores,
equipamentos para processamento e transmissão de dados, aeronaves, espaçonaves
e etc., com o objetivo de estudar o ambiente terrestre através do registro e da
análise das interações entre a radiação eletromagnética e as substâncias
componentes do planeta Terra, em suas mais diversas manifestações.
1 - Fontes de
energia eletromagnética:
Natural: O Sol é a
principal fonte de energia eletromagnética. Toda matéria a uma
temperatura
absoluta acima de (0º K) emite energia, podendo ser considerada como uma fonte
de radiação.
Artificial: Câmaras com flash,
sensores microondas
2 - Energia
eletromagnética
A
forma mais conhecida da energia eletromagnética é a luz visível, embora outras formas
como raios X, ultravioleta, ondas de rádio e calor também sejam familiares.
Todas essas formas
além de outras menos conhecidas são basicamente da mesma natureza e sua forma
de propagação pode ser explicada através de duas teorias. Uma teoria é
conhecida como “Modelo Corpuscular” e preconiza que a energia se propaga pela
emissão de um fluxo de partículas (fótons). Outra, é conhecida como “Modelo Ondulatório”
e postula que a propagação da energia se faz através de um movimento ondulatório.
Esta teoria descreve a energia eletromagnética como uma feição sinuosa harmônica
que se propaga no vácuo à velocidade da luz, ou seja, 3x108 m/s.
Uma carga elétrica
produz ao seu redor um campo elétrico (E). Quando essa carga entra em movimento
desenvolve-se ao seu redor uma corrente eletromagnética. A aceleração de uma
carga elétrica provoca perturbações nos campos elétrico e magnético, que se propagam
repetitivamente no vácuo.
Uma onda
eletromagnética pode então ser definida como a oscilação do campo elétrico (E)
e magnético (M) segundo um padrão harmônico de ondas, ou seja, espaçadas repetitivamente
no tempo.
Duas
características importantes das ondas eletomagnéticas:
- Comprimento de
onda: É
a distância entre dois picos consecutivos de ondas eletromagnéticas. Por
exemplo, os sensores da faixa do visível apresentam comprimento de onda que
variam de 0,38 ìm a 0,78 ìm.
l®mm onde,
1 ìm = 1x10-6
m
Frequência: Nº de picos que
passa por um determinado ponto numa unidade de tempo.
A frequência é
diretamente proporcional à velocidade de propagação da radiação, mas como essa
velocidade é constante para um mesmo meio de propagação, para que haja
alteração na frequência é necessário que haja alteração no comprimento de onda
(ë).
V = ë x f ⇒ ë = V/f
onde, V = veloc. da luz = 300.000 Km/s
f = frequência, medida em Hertz (Hz)
O espectro eletromagnético
Pode
ser ordenado em função do seu comprimento de onda ou de sua frequência.
O espectro
eletromagnético se estende desde comprimentos de onda muito curtos associados a
raios cósmicos até ondas de rádio de baixa frequência e grandes comprimentos de
onda.
As características
de cada elemento observado determinam a maneira particular segundo a qual emite
ou reflete energia, ou seja, a sua “assinatura” espectral. Um grande nº de
interações torna-se possível quando a energia eletromagnética entra em contato com
a matéria. Essas interações produzem modificações na energia incidente, assim,
ela pode ser:
- Transmitida: Propaga-se através
da matéria
- Absorvida: Cede a sua
energia, sobretudo no aquecimento da matéria
- Refletida: Retorna sem
alterações da superfície da matéria à origem
- Dispersa: Deflectida em
todas as direções e perdida por absorção e por novas deflexões
- Emitida: Geralmente
reemitida pela matéria em função da temperatura e da estrutura molecular
Reflectância
espectral: É
a comparação entre a quantidade de energia refletida por um
alvo e a incidente sobre
ele.
Esse comportamento
por qualquer matéria, é seletivo em relação ao comprimento de onda, e específico
para cada tipo de matéria, dependendo basicamente de sua estrutura atômica e
molecular. Assim, em princípio, torna-se possível a identificação de um objeto
observado por um sensor, através da sua “assinatura espectral”.
curso de engenharia geografica na faculdade de ciencia
Nota
histórica do curso de engenharia geografica na faculdade de ciencia
A faculdade de ciencia foi criada em 1963 para instalação
dos estudos gerais universitários de angola, ministrando apenas os
preparatórios médico-cirúgico, e os cursos de engenharia , agronomia e
silvicultura, medicina veterinária e ciencias pedagogicas.
O decreto- lei n: 48/90, de 28 de Dezembro de 1968
transformou os estudos gerais universitários de angola em universidade de
luanda. Com esta transformação as licenciaturas passaram a ser ministradas
totalmente em angola, pois com os estudos gerais era necessário terminar os
cursos em portugal.
Só em 1968 comecou a funcionar os cursos propriamente
ditos da faculdade, saber.
Biologia
Engenharia geografica
Fisica
Geologia
Matematica
Quimica
O decreto – lei n: 98/70, de 13 de março na universidade
de luanda . o director dos cursos de ciencias. A universidade passa a
designar-se universidade de angola.
Os preparatórios médicos foram extintos (pelo menos a
designação) ficando as chamadas ciencias básicas da medicina a funcionar nesta
faculdade a partir de 1970.
Os preparatórios da engenharia no ano de 1978, passaram a
ser ministrados directamente na quela faculdade.
De 1960 a 1975 funcionou na cidade do lubango, uma secção
com designação de secção de matemática e engenharia geográfica de sá da
bandeira na total dependencia da faculdade de ciencias em luanda, para
ministrar os cursos de matemática e engenharia geográfica. Esta secção passou
teoricamente em 1975 para departamento autónomo para ministrar. Matemática aplicada,
engenharia geográfica e matemática(ramo ensino) mas os acontecimentos politicos
que antecederam a independencia, levaram ao seu encerramento.
quarta-feira, 14 de janeiro de 2015
GENERALIZAÇÃO CARTOGRÁFICA
GENERALIZAÇÃO CARTOGRÁFICA
No domínio convencional da Cartografia generalização cartográfica é
um processo dependente da escala que inclui seleção, simplificação e síntese
dos objetos que devem compor um certo mapa. É um processo claramente voltado à
visualização ou à comunicação eficiente daquilo que está representado num mapa.
Como regra geral, a complexidade de um mapa deve diminuir com a escala do mapa.
Com o advento da tecnologia de SIG, generalização cartográfica passou a
incorporar também a noção de modelagem, que envolve a derivação de uma base de
dados menos complexa para atender a uma certa finalidade. Esta seção dedica-se
à discussão do papel da generalização cartográfica no domínio digital.
Generalização pode ser entendida como o processo de
universalização do conteúdo de uma base de dados espaciais com uma certa
finalidade. Um de seus objetivos deve ser a redução da complexidade, quer seja
para fins de visualização, quer seja para armazenar na base de dados apenas
aquilo que é necessário. A redução da complexidade deve levar em conta uma
certa lógica que não comprometa a exatidão de posicionamento e a exatidão de
atributos dos dados (reveja a seção 2.5 em caso de dúvidas). Algumas das
motivações da generalização são ilustradas na figura.
No domínio digital a
resolução espacial da base de dados parece ser uma dimensão mais relevante que
a escala, de modo que a resolução espacial é, tal e qual a escala o é no
domínio analógico, um dos elementos de controle para a generalização. Pode-se
dizer que a modelagem em níveis de abstração diferentes depende da resolução
espacial. Na verdade, a escala também se torna um elemento de controle quando
há preocupação com visualização dos dados digitais na tela do computador. Neste
caso, exatamente como nos mapas em papel, o objetivo é fazer a comunicação
visual dos dados de forma eficiente.
Uma maneira mais prática de entender generalização
no domínio digital é conceituá-la como a seleção e representação simplificada
de objetos através de transformações espaciais e de atributos. Generalização
afeta diretamente a construção e a derivação de bases de dados. Vista como uma
sequência de transformações, a generalização pode propiciar aumento de robustez
e otimização computacional. Como já foi mencionado, generalização tem um
compromisso forte com eficiência na comunicação visual.
Assinar:
Postagens (Atom)